ベイズ確率の概要

　　ベイズ確率は、ベイズ理論によって提供される確率の解釈の一つであり、確率をある人がある命題に対する信頼の程度として定義する概念を採用しています。ベイズ理論はまた、ベイズの定理を新しい情報に基づいて既存の信頼度を導出または更新する規則として使用できることを提案しています。

ベイズ確率の歴史

　　ベイズ理論とベイズ確率は、トーマス・ベイズ（1702－1761）にちなんで名付けられました。彼は現在ベイズの定理と呼ばれる特殊なケースを証明しました。「ベイズ」という用語は1950年頃から使われ始めましたが、ベイズ自身が彼の名前が付けられたこの非常に広義の確率の解釈を支持するかどうかは定かではありません。ピエール・シモン・ラプラスはベイズの定理のより一般的なバージョンを証明し、天体力学や医学統計の問題、場合によっては法理学の問題を解くためにそれを使用しました。しかし、ピエール・シモン・ラプラスはこの定理が確率論にとって重要であるとは考えていませんでした。彼は依然として確率の古典的な解釈を使い続けました。

　　フランク・P・ラムゼイは『数学の基礎』（1931年）の中で、初めて主観的な信頼度を確率の解釈の一つとして提案しました。ラムゼイはこの解釈を当時より広く受け入れられていた確率の頻度解釈の補足と見なしていました。統計学者のブルーノ・デ・フィネッティは1937年にラムゼイの見解を採用し、確率の頻度解釈の代替案として使いました。L・J・サヴァジは『統計学の基礎』（1954年）の中でこの考えをさらに発展させました。

　　有人试图将“置信度”的直观概念进行形式化的定义和应用。最普通的应用是基于打赌:置信度反映在行为主体愿意在命题上下注的意愿上。

　　信頼に程度がある場合、確率計算の定理は信頼の合理性の程度を測定します。これは、一階論理の定理が信頼の合理性の程度を測定するのと同じようなものです。多くの人は、信頼度を古典的な真値（真または偽）の拡張と見なしています。

　　ハロルド・ジェフリーズ、リチャード・T・コックス、エドウィン・ジェインズ、I・J・グッドはベイズ理論を探究しました。他の著名なベイズ理論の支持者には、ジョン・メイナード・ケインズやB・O・クープマンが含まれます。

ベイズ確率の変種

　　用語：主観的確率、個人確率、認識確率、論理的確率は、通常ベイズ学派と呼ばれる考え方のいくつかを表しています。これらの概念は重複する部分がありますが、それぞれ異なる側面に重点を置いています。ここで挙げた人物の中には、自分自身をベイズ学派と自称しない人もいます。

　　ベイズ確率は、ある個人が不確定な命題に対する信頼の程度を測定するものであり、この意味で主観的なものです。ベイズ学派と自称する人の中には、この主観性を受け入れない人もいます。客観主義学派の主要な代表者は、エドウィン・トンプソン・ジェインズとハロルド・ジェフリーズです。おそらく現在生きている主要な客観的ベイズ学派の人物は、デューク大学のジェームズ・バージャーです。ホセ・ベルナルドや他の一部の人は、ある程度の主観性を認めつつも、多くの実際の状況で「事前参照（reference priors）」を使用する必要性を信じています。

　　論理的（または客観的認識）確率の支持者、例えばハロルド・ジェフリーズ、ルドルフ・カルナップ、リチャード・スレルケルド・コックス、エドウィン・ジェインズは、ある不確定な命題の真実性に関する同じ情報を持つ二人の人が同じ確率を計算できる技術を規則化したいと考えています。この確率は個人に関係なく、認識状況のみに関係するため、主観と客観の中間に位置します。しかし、彼らが提案する方法には議論の余地があります。批判者はこの主張に異議を唱え、関連する事実の情報が不足している場合、ある信頼度を選ぶことに現実的な根拠があると主張しています。もう一つの問題は、これまでの技術では実際の問題を解決するには不十分であるということです。

ベイズ確率と頻度確率

　　ベイズ確率は頻度確率と対照的で、確定した分布から観測された頻度や標本空間内の割合から確率を導出します。

　　頻度確率を採用した統計学と確率論は、R・A・フィッシャー、エゴン・ピアソン、イェジ・ネイマンによって20世紀前半に発展させられました。A・N・コルモゴロフも頻度確率を使って、ルベーグ積分によって測度論における確率の数学的基礎を築きました（『確率論の基礎』(1933年)）。サヴァジ、クープマン、アブラハム・ワルドや他の学者たちは1950年以降、ベイズ確率を発展させました。

　　ベイズ学派と頻度学派の確率解釈の違いは、統計学の実践に重要な影響を与えます。例えば、同じデータを使って二つの仮説を比較する場合、仮説検定理論は確率の頻度解釈に基づいており、誤ってデータが別のモデル/仮説を支持する確率に基づいて、あるモデル/仮説（帰無仮説）を否定または受け入れることができます。このような誤りが発生する確率を第一種誤差と呼び、これには実際に観測されたデータよりも極端な仮想的なデータ集合を同じデータ源から導出することを考慮する必要があります。この方法により、「二つの仮説が異なるか、または観測されたデータが誤解を招く集合である」という主張が可能になります。これに対して、ベイズ方法は実際に観測されたデータに基づいているため、任意の数の仮説に対して直接事後確率を与えることができます。各仮説を表すモデルのパラメータに確率を与える必要があることは、この直接的な方法の代償です。

ベイズ確率の応用

　　1950年代以降、ベイズ理論とベイズ確率はコックスの定理、ジェインズの最大エントロピー原理、そしてオランダブック論証によって広く応用されています。多くの応用において、ベイズ方法はより普遍的であり、頻度確率よりも良い結果をもたらすように見えます。ベイズ因子はまた、オッカムの剃刀とともに使用されます。数学的な応用については、ベイズ推論とベイズの定理を参照してください。

　　一部の人は、ベイズ推論を科学的方法の一つの応用と見なしています。なぜなら、ベイズ推論によって確率を更新するには、異なる仮説に対する初期の信頼度から始め、新しい情報を収集し（例えば実験を行うことによって）、その後新しい情報に基づいて元の信念を調整する必要があるからです。元の信念を調整することは、初期の仮説を（より近づけて）受け入れるか、または棄却することを意味するかもしれません。

　　ベイズ技術は最近、スパムメールのフィルタリングに応用されています。ベイズスパムフィルタは、電子メールの参照集合を使って、最初にスパムメールと見なされるものを定義します。参照を定義した後、フィルタは参照内の特徴を使って、新しいメールをスパムメールまたは有効なメールとして判定します。新しい電子メールが新しい情報として現れ、ユーザーがスパムメールと有効なメールの判定に誤りを発見した場合、この新しい情報は初期の参照集合内の情報を更新し、将来の判定をより正確にすることを目指します。ベイズ推論とベイズフィルタリングを参照してください。

確率の確率

　　ベイズ確率の解釈に対する批判の一つは、単一の確率の割り当てが信念の真実性、つまりそれがどれだけの科学的実証を持っているかを示すことができないということです。次のような状況を考えてみましょう。

1. 白い玉と黒い玉が入った箱がありますが、それらの数はわかりません。

2. 箱があり、そこからn個の玉を取り出しました。半分は黒、半分は白です。

3. 箱があり、黒い玉と白い玉の数が同じであることがわかっています。

次に取り出す玉が黒玉であるベイズ確率は、すべての三つの場合で0.5になります。ケインズはこれを「証拠の重み」の問題と呼んでいます。これらの証拠の支持の違いを反映する方法は、これらの確率自体に確率（いわゆる「メタ確率」）を割り当てることです。以下の通りです。

• 1. 白い玉と黒い玉が入った箱がありますが、数はわかりません。

• 
  

• 次の玉が黒玉である確率がpであることを表す命題をθ = pとします。ベイズ確率論者は、Β事前分布を割り当てます。

• 

• 

• 
  

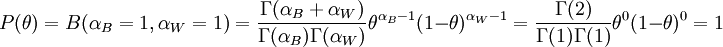
• 取り出した玉を二項分布でモデル化すると仮定すると、m