自己組織化マップ（Self - organizing map, SOM）は、入力空間のデータを学習することで、低次元で離散的なマップ（Map）を生成し、ある意味で次元削減アルゴリズムとも見なせます。

SOMは教師なしの人工ニューラルネットワークです。一般的なニューラルネットワークが損失関数に基づく逆伝播で学習するのと異なり、競合学習（competitive learning）戦略を用いて、ニューロン間の競合により徐々にネットワークを最適化します。また、近傍関数（neighborhood function）を使用して入力空間のトポロジー構造を維持します。

入力空間のトポロジー構造を維持するとは、2次元マップにデータ点間の相対距離が含まれることを意味します。入力空間で隣接するサンプルは、隣接する出力ニューロンにマッピングされます。

教師なし学習に基づいているため、学習段階で人為的な介入（サンプルラベルが不要）が必要なく、クラスを知らない状態でデータをクラスタリングしたり、ある問題に内在する関連特徴を識別したりできます。

特徴のまとめ：

• ニューラルネットワーク、競合学習戦略

• 教師なし学習、追加のラベル不要

• 高次元データの可視化に非常に適しており、入力空間のトポロジー構造を維持できる

• 高い汎化能力を持ち、これまでに遭遇したことのない入力サンプルも識別できます
  

オンライン上には多くのオープンソースの実装があり、ここに私がgithubで収集したリストを示します：

理論だけで話すことで分かりにくくなるのを避けるために、miniSomライブラリの一部の実装を例にして、学習過程のいくつかの式を理解するのを助けます。

ネットワーク構造

SOMのネットワーク構造は2層あります：入力層、出力層（競合層とも呼ばれます）

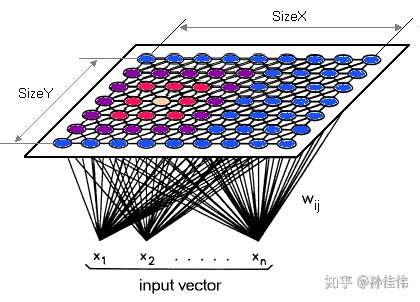
入力層のニューロンの数は入力ベクトルの次元によって決まり、1つのニューロンが1つの特徴に対応します。

SOMネットワーク構造の違いは主に競合層にあります：1次元、2次元（最も一般的）があります。

競合層はより高い次元にすることもできます。ただし、可視化の目的から、高次元の競合層はあまり使われません。

このうち、2次元平面には2種類の平面構造があります：

• Rectangular（矩形）

• Hexagonal（六角形）

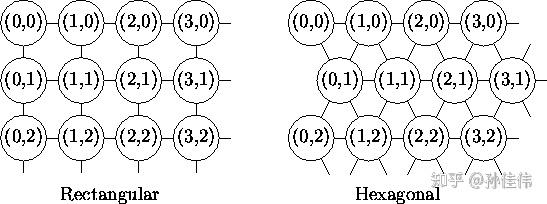
競合層のSOMニューロンの数は、最終モデルの粒度と規模を決定します。これは最終モデルの精度と汎化能力に大きな影響を与えます。

経験則の式：

競合層の最少ノード数 =  

N：学習サンプルの数

正方形の出力層の場合、辺の長さは競合層のノード数の平方根を切り上げた値になります。

学習計算過程

第一步：他のニューラルネットワークと同じく、重み（Weighs）を小さな乱数で初期化する必要があります。

第二步：ランダムに1つの入力サンプルXiを選びます。

第三步：

1. 競合層の各ノードを走査し、Xiとノード間の類似度（通常はユークリッド距離を使用）を計算します。

2. 距離が最小のノードを勝者ノード（winner node）として選び、時にはBMU（best matching unit）とも呼ばれます。

第四步：近傍半径σ（sigma）に基づいて勝者近傍に含まれるノードを決定し、近傍関数（neighborhood function）を通じてそれぞれの更新幅を計算します（基本的な考え方は、勝者ノードに近いほど更新幅が大きく、遠いほど更新幅が小さくなります）。

第五步：勝者近傍内のノードの重み（Weight）を更新します：

W_v(s + 1) = W_v(s) + θ(u, v, s) · α(s) · (D(t) - W_v(s))

θ(u, v, s)は更新の制約で、BMUからの距離に基づいた近傍関数の返り値です。
W_v(s)はノードvの現在の重みです。

第六步：1回の反復を完了し（反復回数 + 1）、第二步に戻り、設定された反復回数に達するまで繰り返します。

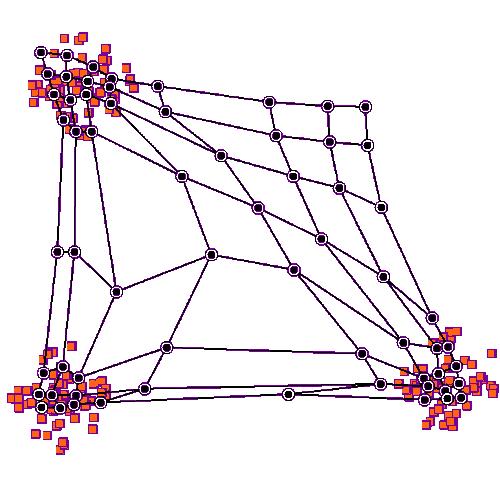
gifで示される学習過程のように、勝者ノードは更新後、入力サンプルXiの空間内の位置に近づきます。勝者ノードのトポロジー上の近傍ノードも同様に更新されます。これがSOMネットワークの競合調整戦略です。

近傍関数（neighborhood function）

近傍関数は、勝者ノードが近傍ノードに与える影響の強さ、つまり勝者近傍内の各ノードの更新幅を決定するために使用されます。最も一般的な選択はガウス関数で、勝者近傍内での影響の強さと距離の関係を表すことができます。

g = neighborhood_func(winner, sigma) 
w_new = learning_rate * g * (x - w)

winnerは勝者ノードの出力平面上の座標です。

sigmaは近傍範囲を決定し、sigmaが大きいほど近傍範囲が広くなります。

sigmaの取りうる値の範囲：

• sigmaは0より大きくなければならず、そうでないとニューロンが更新されません。

• また、sigmaは2次元出力平面の辺の長さより大きくすることはできません。

ガウス関数には指数項が含まれるため、計算量が非常に大きくなります。bubble関数を使ってガウス関数をよく近似することができます。bubble関数は勝者ノードの近傍範囲内では定数であるため、近傍内のすべてのニューロンの更新幅は同じになります。sigmaによってのみ、どれだけのニューロンが更新に関与するかが決まります。

bubble関数は、計算コストとガウスカーネルの精度のバランスをうまく取ることができます。

勝者近傍内のノードの更新程度の可視化：

5X5の競合層を例にとり、中心ノードが勝者ノードであると仮定します。

from numpy import outer, logical_and
size = 5
neigx = arange(size)
neigy = arange(size)

ガウス近傍関数：

ガウス関数は連続的であるため、sigmaの有効な取りうる値の範囲も連続的です。

def gaussian(c, sigma):
    """Returns a Gaussian centered in c."""
    d = 2*pi*sigma*sigma
    ax = exp(-power(neigx - c[0], 2)/d)
    ay = exp(-power(neigy - c[1], 2)/d)
    return outer(ax, ay)  # the external product gives a matrix

out = gaussian((2,2),1)

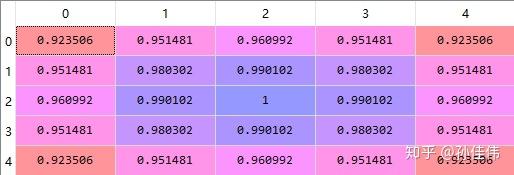
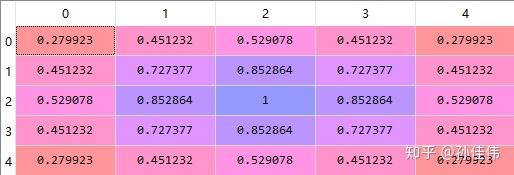sigma = 1

sigmaを1に設定すると、すべてのノードに一定の更新幅があり、中心の勝者ノードは1で、勝者ノードから遠ざかるほど更新幅が低くなります。

sigmaは実際にはこの距離による減衰の程度を制御しています。

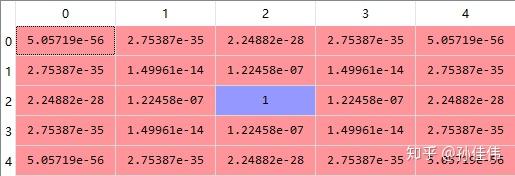sigma = 0.1

sigmaの値が非常に小さい場合、勝者ノードの更新幅のみが1で、他のノードはほとんど0に近くなります。

sigma = 4

sigmaの値が大きい場合、減衰の程度は遅く、端のノードでも比較的大きな更新幅があります。

Bubble近傍関数：

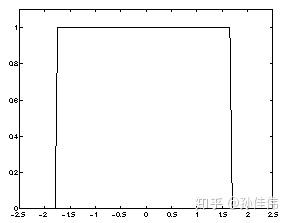
Bubble関数：勝者近傍内のニューロンは、更新係数がすべて同じです。

(X > winner_x - sigma) & (X < winner_x + sigma)

したがって、     sigmaの有効な取りうる値は離散的です：

0.5：勝者ノードのみ

1.5：周囲1周

2.5：周囲2周

(1,2] の間の値はすべて同じ効果で、周囲1周になります。

def bubble( c, sigma):
    "