K-Meansクラスタリングアルゴリズムは、皆さんが最もよく知っているクラスタリングアルゴリズムかもしれません。これは多くの入門的なデータサイエンスや機械学習の講座に登場します。コードで理解し、実装するのは簡単です！下のグラフを見てください。

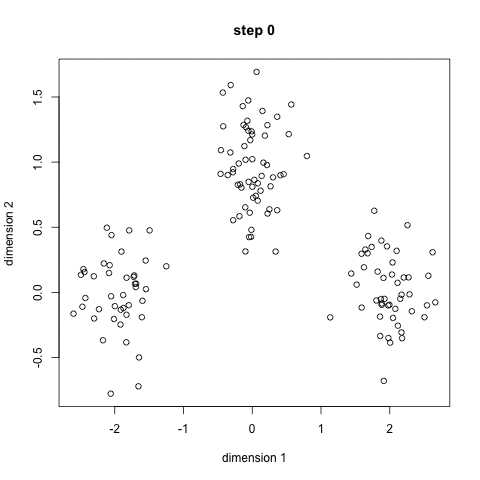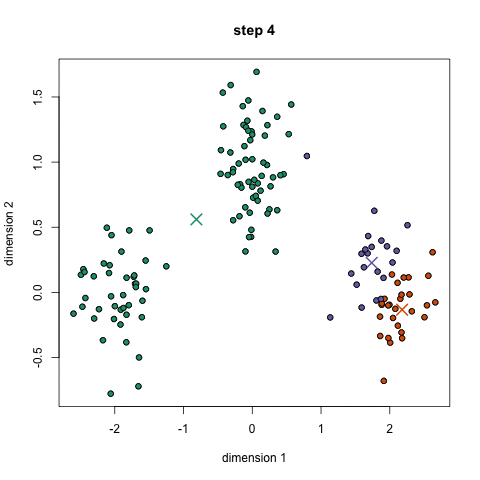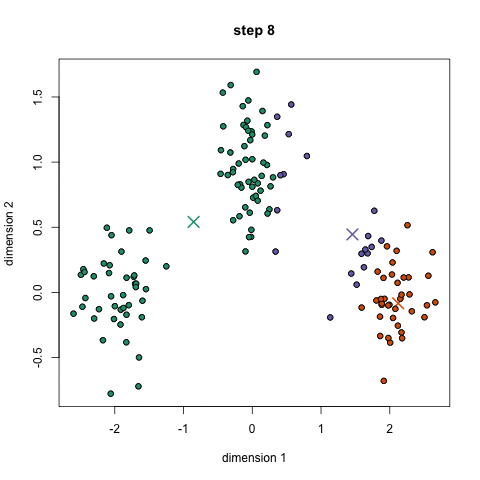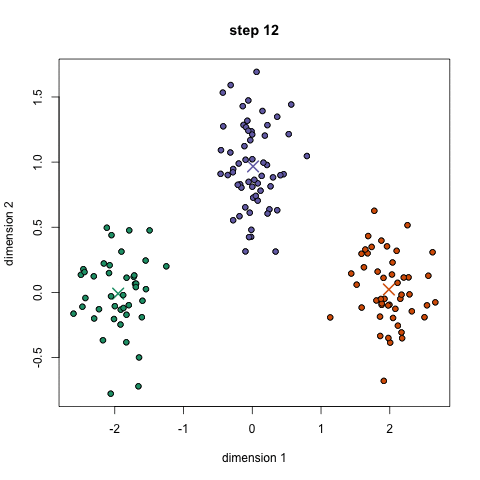
K-Meansクラスタリング

1.まず、使用するクラス/グループをいくつか選択し、それぞれの中心点をランダムに初期化します。使用するクラスの数を知るには、データをすばやく見て、異なるグループ分けを試してみるのが良いです。中心点は、各データ点のベクトルと同じ長さのベクトルで、上のグラフでは「X」です。

2.各データ点は、点と各グループの中心との間の距離を計算することで分類され、その点は最も近いグループに分類されます。

3.これらの分類点に基づいて、グループ内のすべてのベクトルの平均を取ることで、グループの中心を再計算します。

4.これらの手順を一連の反復で繰り返します。また、グループの中心をランダムに何度か初期化し、最良の結果を提供したと思われるものを選んで実行することもできます。

K-Meansクラスタリングアルゴリズムの利点は、非常に高速であることです。なぜなら、私たちが行っているのは点とグループの中心との間の距離を計算するだけであり、線形の計算量O(n)があるからです。

一方、K-Meansにはいくつかの欠点もあります。まず、いくつのグループ/クラスを選択するかを決めなければなりません。これは重要ではないことではありません。理想的には、データから何らかの示唆を得ることが重要であるため、これらの問題を解決してくれることが望まれます。K-Meansはまた、ランダムに選択されたクラスタ中心から始まるため、異なるアルゴリズムの実行では異なるクラスタリング結果が得られる可能性があります。したがって、結果は再現性がなく、一貫性に欠けることがあります。他のクラスタリング方法はより一貫性があります。

K-Mediansは、K-Meansに関連する別のクラスタリングアルゴリズムです。グループの中心点を再計算するために平均の中央値を使用することを除いて、この方法は外れ値に対する敏感度が低く（中央値を使用するため）、大規模なデータセットに対しては、中央値ベクトルを計算する際に各反復でソートが必要になるため、はるかに遅くなります。