DBSCAN（Density-based Spatial Clustering of Applications with Noise：ノイズを含むアプリケーションの密度ベース空間クラスタリング）は、比較的代表的な密度ベースのクラスタリングアルゴリズムです。平均シフトクラスタリングアルゴリズムに似ていますが、いくつかの顕著な利点があります。

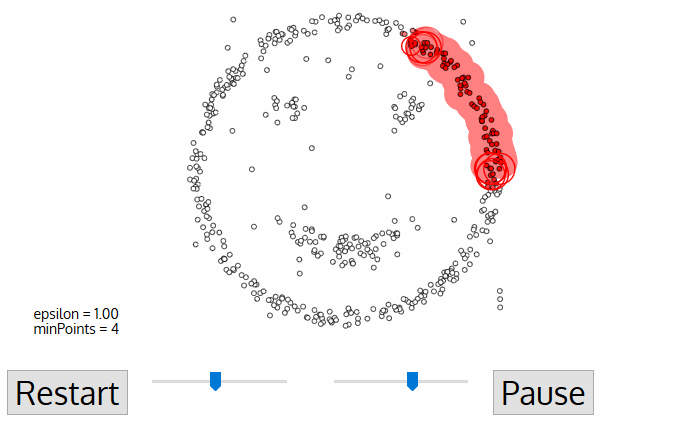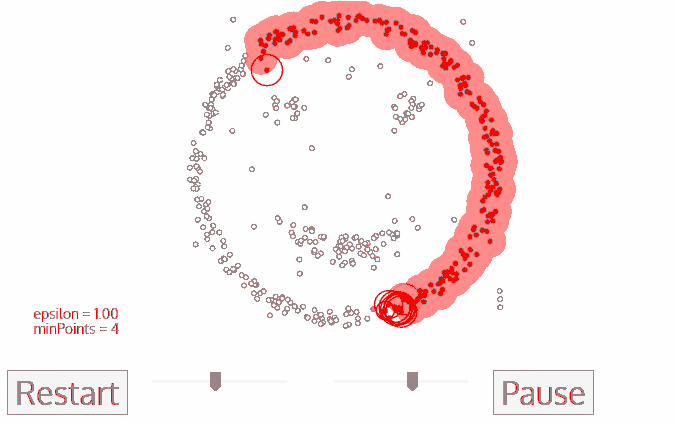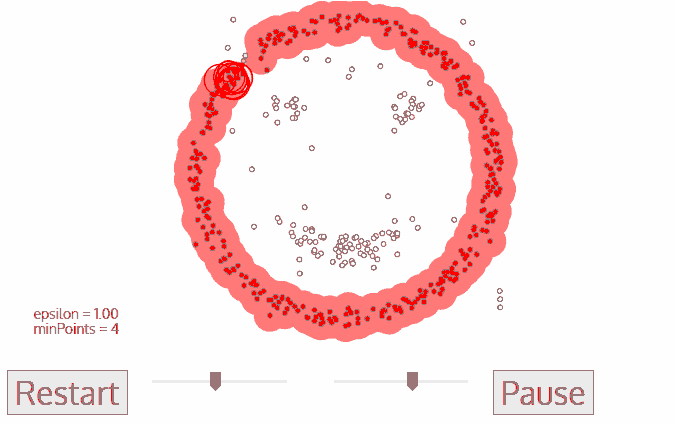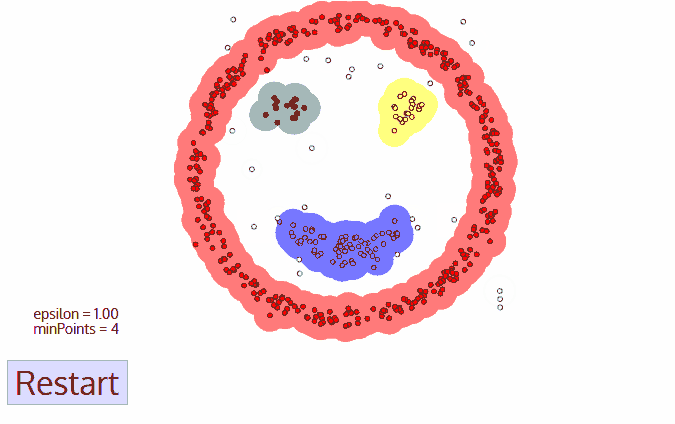
DBSCANによる笑顔のクラスタリング

1. DBSCANは、未訪問の任意のデータ点から始まります。この点の近傍は、距離ε（ε距離内のすべての点が近傍点）を用いて抽出されます。

2. この近傍に十分な数の点がある場合（minPointsに基づく）、クラスタリングプロセスが開始され、現在のデータ点が新しいクラスタの最初の点になります。そうでない場合、その点はノイズとしてマークされます（後でこのノイズ点がクラスタの一部になる可能性があります）。どちらの場合も、この点は「訪問済み（visited）」としてマークされます。

3. 新しいクラスタの最初の点に対して、そのε距離内の点も同じクラスタの一部になります。このプロセスにより、ε近傍のすべての点が同じクラスタに属するようになり、クラスタグループに新しく追加されたすべての点に対してこの操作が繰り返されます。

4. ステップ2とステップ3のプロセスは、クラスタ内のすべての点が確定するまで繰り返されます。つまり、クラスタの近傍のすべての点が訪問され、マークされるまでです。

5. 現在のクラスタリングが完了すると、新しい未訪問点が検索され、処理され、さらなるクラスタまたはノイズが発見されます。このプロセスは、すべての点が訪問済みとしてマークされるまで繰り返されます。すべての点が訪問された後は、各点はクラスタに属するか、ノイズとしてマークされます。

DBSCANは他のクラスタリングアルゴリズムに比べていくつかの利点があります。まず、事前にクラスタ数を設定する必要がありません。また、異常値をノイズとして識別しますが、平均シフトクラスタリングアルゴリズムのように、データ点が非常に異なっていてもクラスタに含めることはありません。さらに、任意のサイズと形状のクラスタをうまく見つけることができます。

DBSCANの主な欠点は、クラスタの密度が異なる場合、他のクラスタリングアルゴリズムほど性能が良くないことです。これは、密度が変化すると、距離閾値εと近傍点を識別するminPointsの設定がクラスタによって異なるためです。この欠点は、非常に高次元のデータでも発生します。なぜなら、距離閾値εを推定するのが難しくなるからです。

ガウス混合モデル（GMM）を用いた期待値最大化（EM）クラスタリング

K-Meansの主な欠点の1つは、クラスタ中心の平均値の使用が単純で幼稚であることです。以下の画像を見ることで、なぜこれが最善の方法ではないかを理解できます。左側の画像では、同じ平均値を中心とする異なる半径の2つの円形のクラスタがあることが明らかです。K-Meansはこれを処理できません。なぜなら、クラスタの平均値が非常に近いからです。クラスタが円形でない場合も、K-Meansは失敗します。これも、平均値をクラスタ中心として使用する結果です。

K-Meansの2つの失敗例

ガウス混合モデル（GMMs）はK-Meansよりも柔軟性が高いです。ガウス混合モデルを使用すると、データ点がガウス分布していると仮定できます。これは、データ点が円形であるという仮定よりも緩やかな仮定です。このように、クラスタの形状を記述するために2つのパラメータ（平均値と標準偏差）があります。2次元の例では、これはクラスタが任意の楕円形状をとることができることを意味します（xとy方向にそれぞれ標準偏差があるため）。したがって、各ガウス分布は個別のクラスタに帰属することができます。

各クラスタのガウス分布のパラメータ（例えば平均値と標準偏差）を見つけるために、期待値最大化（EM）と呼ばれる最適化アルゴリズムを使用します。以下のグラフを見ると、ガウス混合モデルがクラスタに適合していることがわかります。その後、期待値最大化のプロセスを続けることができます。つまり、ガウス混合モデルを使用してクラスタリングを最大化します。

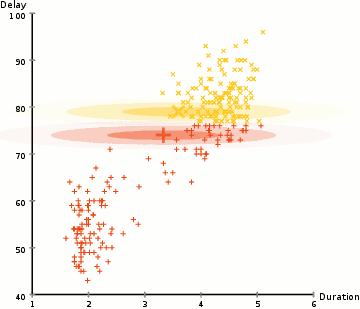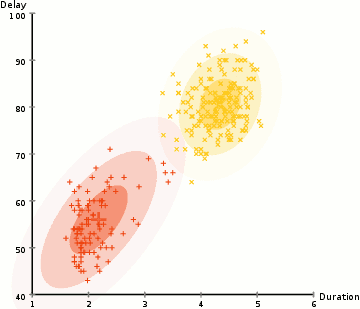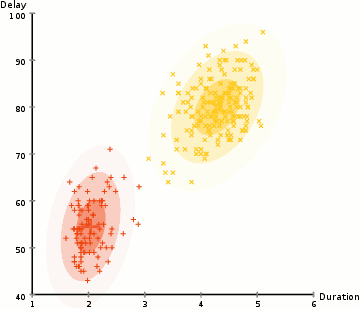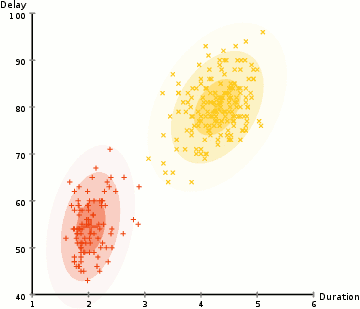
ガウス混合モデルを用いた期待値最大化クラスタリング

1. まず、クラスタ数を選択し（K-Meansと同じように）、各クラスタのガウス分布のパラメータをランダムに初期化します。データを素早く見ることで、初期パラメータを適切に推測することができます。ただし、上のグラフにあるように、これは必ずしも100％必要ではありません。なぜなら、ガウス分布が最初は非常に悪い状態で始まっても、すぐに最適化されるからです。

2. 各クラスタのガウス分布が与えられた場合、各データ点が特定のクラスタに属する確率を計算します。ある点がガウス分布の中心に近いほど、そのクラスタに属する確率が高くなります。これは直感的です。なぜなら、ガウス分布を仮定すると、ほとんどのデータはクラスタ中心の近くにあると考えられるからです。

3. これらの確率に基づいて、ガウス分布の新しいパラメータを計算します。これにより、クラスタ内のデータ点の確率を最大限に利用することができます。新しいパラメータは、データ点の位置の加重和を用いて計算されます。重みは、特定のクラスタに属するデータ点の確率です。これを説明するために、上の図、特に黄色のクラスタを例に見てみましょう。最初の反復では分布はランダムですが、ほとんどの黄色の点がこの分布の右側にあることがわかります。確率で重み付けされた和を計算すると、中心付近にいくつかの点があっても、大部分は右側にあります。したがって、自然に分布の平均値はこれらの点に近くなります。また、ほとんどの点が「右上から左下」に分布していることがわかります。したがって、標準偏差はこれらの点に合った楕円を作成するように変化し、確率の合計が最大化されます。

ステップ2と3は、収束するまで反復して繰り返されます。収束とは、分布が反復ごとに大きく変化しなくなる状態を指します。

ガウス混合モデルを使用することには2つの重要な利点があります。まず、ガウス混合モデルは、クラスタの共分散に関してK-Meansよりもはるかに柔軟です。標準偏差パラメータに応じて、クラスタは任意の楕円形状をとることができ、円形に限定されません。実際、K-Meansはガウス混合モデルの特殊なケースであり、各クラスタのすべての次元で共分散が0に近い場合に相当します。其次、ガウス混合モデルの使用確率に基づいて、各データ点は複数のクラスタに属することができます。したがって、あるデータ点が2つの重なり合うクラスタの中間にある場合、X％が1クラスに属し、Y％が2クラスに属するというように、簡単にそのクラスを定義することができます。