数学における最適化問題の一般的な表現は、 を求めることで、 となるようにすることです。ここで、 はn次元ベクトルで、 は の実行可能領域で、 は 上の実数値関数です。
凸最適化 問題とは、 が 閉じた凸集合 で、かつ が 上の 凸関数 である最適化問題のことを指します。これら2つの条件のいずれかを満たさない場合、その問題は非凸最適化問題となります。

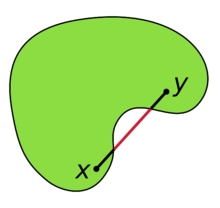
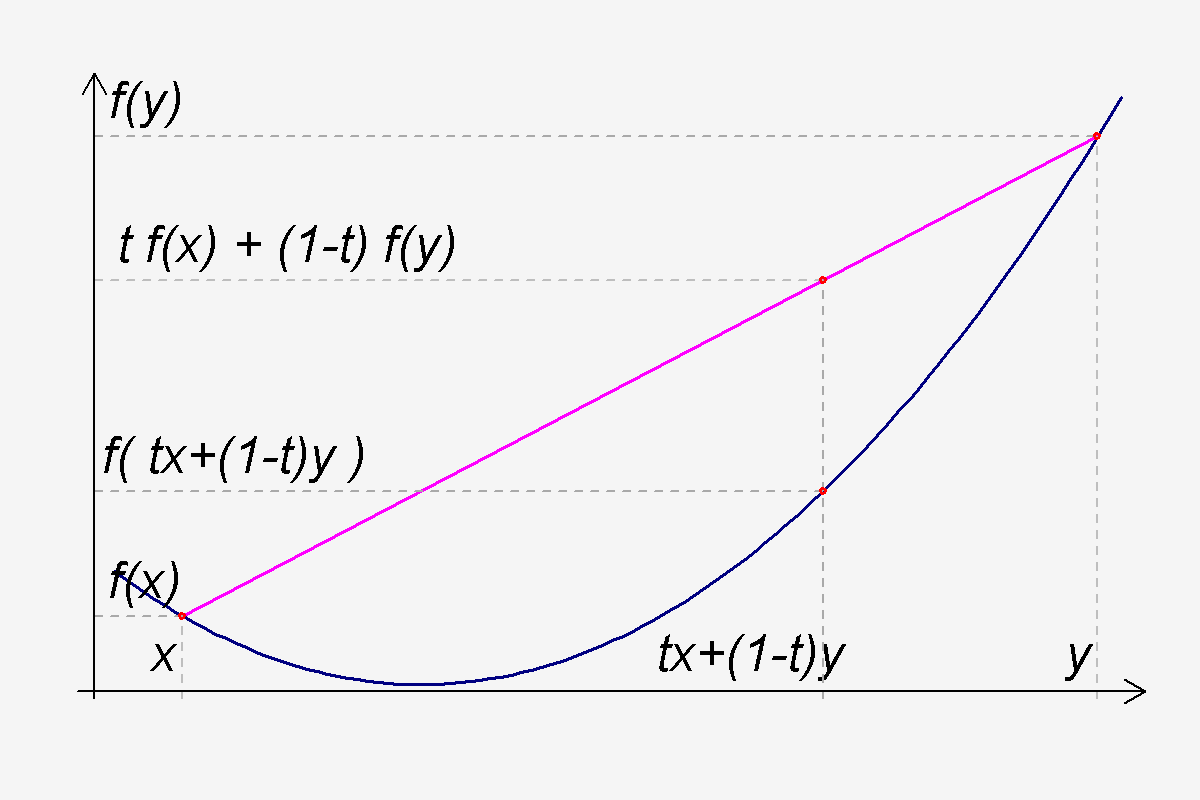
ここで、が 凸集合とは、集合内の任意の2点に対して、が成り立つこと、つまり任意の2点を結ぶ線分が集合内に含まれることを意味します。直感的には、集合に「凹んだ」部分がないようなものです。閉じた凸集合については、閉集合の定義に関連し、閉集合の定義は開集合に基づいているため、やや抽象的ですのでここでは詳述しません。ここでは、閉じた凸集合はすべての境界点を含む凸集合と考えることができます。

•    
  

• 注意：中国大陸の数学界の一部の機関における関数の凹凸性の定義は、海外の定義と逆になっています。Convex Functionは中国大陸の一部の数学書では凹関数を指し、Concave Functionは凸関数を指します。しかし、中国大陸の経済学関連の多くの書籍では、凹凸性の表現は他の国と同じで、つまり数学教材とは逆になっています。例えば、東京工業大学の高等数学教材における関数の凹凸性の定義は、本項目と逆になっています。本項目の凹凸性はその上方図が凹集合または凸集合であることを指し、東京工業大学の高等数学教材ではその下方図が凹集合または凸集合であることを指し、両者の定義は正反対です。  
  

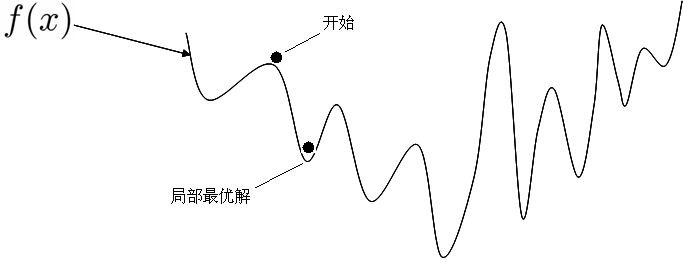
• なぜ凸関数であることが要求されるのでしょうか？   なぜなら、下図のような関数の場合、全体最適解を得ることができないからです。

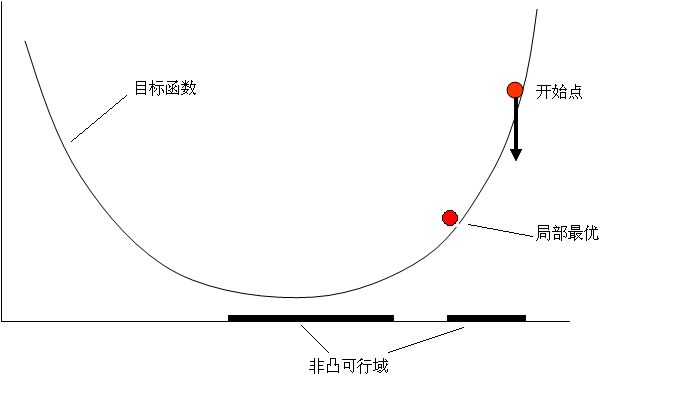
• なぜ凸集合であることが要求されるのでしょうか？なぜなら、実行可能領域が凸集合でない場合、局所最適解に収束してしまうからです。

• 
  

• 実際のモデリングにおいて、最適化問題が凸最適化問題であるかどうかを判断するには、一般的に以下の点を見ます。
  

  凸最適化問題と非凸最適化問題を区別する理由は、凸最適化問題では局所最適解が同時に全体最適解となるという特性があり、この特性により凸最適化問題はある意味で解きやすくなります。一方、一般的な非凸最適化問題はそれに比べて解くのが難しくなります。  
   

• 目的関数が凸関数でない場合、凸最適化問題ではありません。

• 決定変数に離散変数（0 - 1変数または整数変数）が含まれる場合、凸最適化問題ではありません。
  

• 制約条件を

  post
  百科事典の知識
  2021-05-11 23:49:38join communtity

  • 41

    item of content

  人工知能に関する知識を共有します。これにはAIアルゴリズム、応用例、データ、モデルなどに関する情報が含まれます。