ベイズネットワーク（Bayesian network）は、信念ネットワーク（Belief Network）や有向非巡回グラフモデル（directed acyclic graphical model）とも呼ばれ、確率グラフモデルの一種で、1985年にJudea Pearlによって初めて提案されました。これは、人間の推論過程における因果関係の不確定性を扱うモデルで、そのネットワークのトポロジー構造は有向非巡回グラフ（DAG）です。

    ベイズネットワークの有向非巡回グラフのノードは確率変数を表します。これらは観測可能な変数、隠れ変数、未知のパラメータなどです。因果関係（または非条件独立）があると考えられる変数や命題は矢印で結ばれます。2つのノードが1本の矢印で結ばれている場合、一方のノードが「原因（parents）」で、もう一方が「結果（children）」で、2つのノード間には条件付き確率値が生じます。要するに、2つのノードを結ぶ矢印は、この2つの確率変数に因果関係があるか、非条件独立であることを表します。

例えば、ノードEがノードHに直接影響を与えると仮定すると、つまりE→Hであれば、EからHへの矢印でノードEからノードHへの有向弧（E,H）を作成し、重み（つまり結合強度）は条件付き確率P(H|E)で表されます。次の図のように：

     簡単に言えば、ある研究システムに関係する確率変数を、条件独立かどうかに基づいて有向グラフに描くと、ベイズネットワークが形成されます。主に確率変数間の条件付き依存関係を記述するために使われ、円で確率変数（random variables）を表し、矢印で条件付き依存関係（conditional dependencies）を表します。

    有向非巡回グラフ（DAG）をG = (L,E)と表します。ここで、Lはグラフ中のすべてのノードの集合を表し、Eは有向結合線分の集合を表します。また、X = (Xi) i ∈ Lを有向非巡回グラフ中のあるノードiが表す確率変数とします。ノードXの同時確率が次のように表せる場合：

Xを有向非巡回グラフGに関するベイズネットワークと呼びます。ここで、はノードiの「原因」を表し、またはpa(i)はiの親（parents）です。

さらに、任意の確率変数の同時確率は、それぞれの局所的な条件付き確率分布を掛け合わせることで得られます：

次の図のように、簡単なベイズネットワークです：

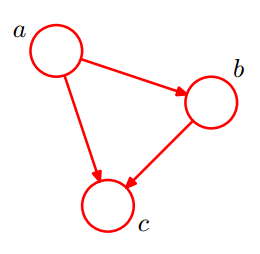
aがbを引き起こし、aとbがcを引き起こすので、次のようになります：

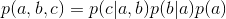
2.2 ベイズネットワークの3つの構造形式

    次の図のようなベイズネットワークが与えられます：

図から直感的に分かることは：

• (1). x1,x2,…x7の同時分布は：

• (2). x1とx2は独立（head-to-headに対応）；

• (3). x6とx7はx4が与えられた条件下で独立（tail-to-tailに対応）。

    上の図に基づいて、1点目は理解しやすいかもしれませんが、2点目と3点目で述べられている条件独立とは何を意味するのでしょうか？実際、2点目と3点目はベイズネットワークの3つの構造形式のうちの2つです。この問題を明確にするために、D-Separation（D-分離）という概念を導入する必要があります。

D-Separationは、変数が条件独立かどうかを判断するためのグラフィカルな方法です。言い換えれば、有向非巡回グラフ（DAG）Eに対して、D-Separation方法では、2つのノード間が条件独立かどうかを迅速に判断できます。

2.2.1 形式1：head-to-head

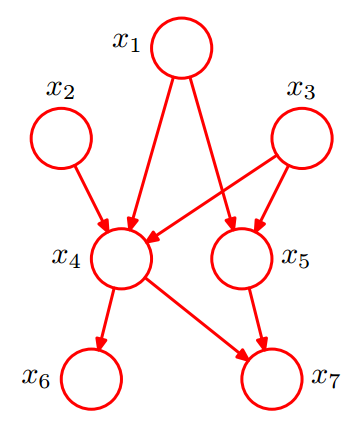
    ベイズネットワークの最初の構造形式は次の図のように：

よって、P(a,b,c) = P(a)*P(b)*P(c|a,b)が成り立ち、簡略化すると：

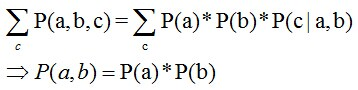
つまり、cが未知の条件下では、aとbは遮断（blocked）され、独立です。これをhead-to-head条件独立と呼び、この節の最初の図の「x1、x2独立」に対応します。

2.2.2 形式2：tail-to-tail

    ベイズネットワークの2番目の構造形式は次の図のように：

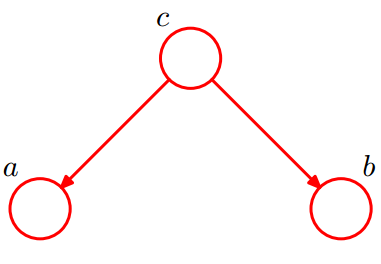
cが未知の場合と、cが既知の場合の2つのケースを考えます：

• cが未知のとき、P(a,b,c)=P(c)*P(a|c)*P(b|c)です。このとき、P(a,b) = P(a)P(b)を導くことはできません。つまり、cが未知のとき、aとbは独立ではありません。

• cが既知のとき、P(a,b|c)=P(a,b,c)/P(c)です。そして、P(a,b,c)=P(c)*P(a|c)*P(b|c)を式に代入すると、P(a,b|c)=P(a,b,c)/