K-Meansの欠点は、クラスタ中心の平均を単純に使用することにあります。下の図の2つの円に対してK-Meansを使用すると、正しいクラスの判断ができません。同様に、データセットの点が下の図の曲線のような場合も、正しく分類できません。

ガウス混合モデル（GMM）を使ってクラスタリングを行う場合、まずデータ点がガウス分布に従っていると仮定します。これに対し、K-Meansはデータ点が円形であると仮定しています。ガウス分布（楕円形）はより多くの可能性を与えます。クラスタの形状を表すために、平均と標準偏差という2つのパラメータがあります。したがって、これらのクラスタは、x、y方向に標準偏差があるため、任意の形状の楕円形をとることができます。したがって、各ガウス分布は単一のクラスタに割り当てられます。
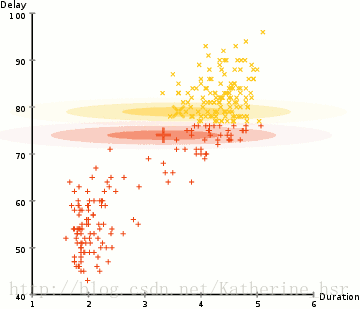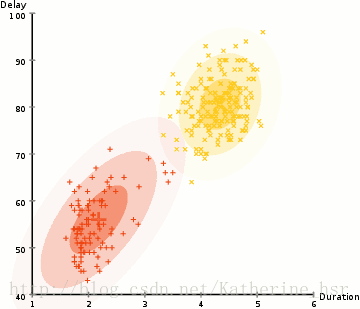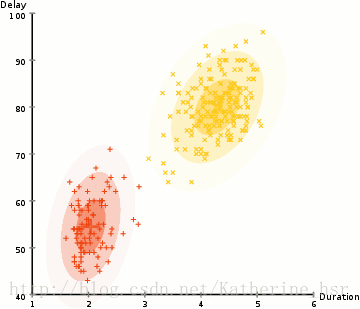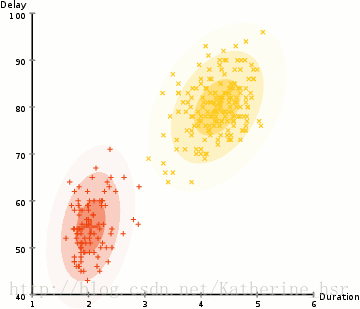
ですから、クラスタリングを行うにはまず、データセットの平均と標準偏差を求める必要があります。ここでは、最大期待値（EM）と呼ばれる最適化アルゴリズムを使用します。下の図は、GMMを使用した最大期待値によるクラスタリングの過程を示しています。

具体的な手順：
1. クラスタの数を選択し（K-Meansと同様）、各クラスタのガウス分布のパラメータ（平均と分散）をランダムに初期化します。また、データを観察して、比較的正確な平均と分散を設定することもできます。
2. 各クラスタのガウス分布が与えられた場合、各データ点が各クラスタに属する確率を計算します。ある点がガウス分布の中心に近いほど、そのクラスタに属する可能性が高くなります。
3. これらの確率に基づいて、データ点の確率が最大化されるようにガウス分布のパラメータを計算します。これらの新しいパラメータは、データ点の確率を重み付けして計算することができます。重みは、データ点がそのクラスタに属する確率です。
4. 2と3を繰り返して、繰り返しの間の変化が小さくなるまで続けます。
GMMの利点：（1）GMMは平均と標準偏差を使用するため、クラスタは円形に限定されず、楕円形をとることができます。K-MeansはGMMの特殊なケースであり、すべての次元で分散が0に近い場合、クラスタは円形になります。
（2）GMMは確率を使用するため、1つのデータ点は複数のクラスタに属することができます。例えば、データ点Xは、Aクラスタに属する確率が20％、Bクラスタに属する確率が80％ということがあります。つまり、GMMは混合資格をサポートしています。

https://blog.csdn.net/weixin_42056745/article/details/101287231