分散とは何か

　　分散と標準偏差は、データのばらつきの程度を測るために最も重要で最もよく使われる指標です。

　　分散は、各データとその算術平均との偏差の二乗和の平均で、通常はσ²で表されます。分散の測定単位や次元は、経済的な意味から解釈するのが不便なので、実際の統計作業では分散の算術平方根である標準偏差を使って統計データの差の程度を測ることが多いです。

　　標準偏差は、平均二乗偏差とも呼ばれ、一般にσで表されます。分散と標準偏差の計算には、単純平均法と加重平均法があり、また、母集団データと標本データでは、公式が少し異なります。

分散の計算公式

　　母集団の分散をσ²とすると、グループ化されていない生データの場合、分散の計算公式は次の通りです。

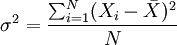
　　グループ化されたデータの場合、分散の計算公式は次の通りです。

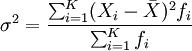
　　分散の平方根が標準偏差で、それに対応する計算公式は次の通りです。

　　グループ化されていないデータ：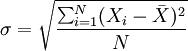

　　グループ化されたデータ：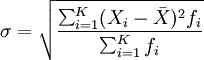

標本分散と標準偏差

　　標本分散と母集団分散の計算上の違いは、母集団分散はデータの個数または総度数で偏差の二乗和を割るのに対し、標本分散は標本データの個数または総度数から1を引いた数で偏差の二乗和を割ることです。ここで、標本データの個数から1を引いたn－1を自由度と呼びます。標本分散を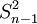とすると、グループ化されていないデータとグループ化されたデータから標本分散を計算する公式はそれぞれ次の通りです。

　　グループ化されていないデータ：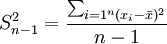

　　グループ化されたデータ：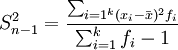

　　グループ化されていないデータ：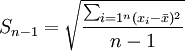

　　グループ化されたデータ：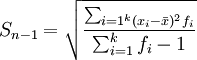

　　例：ある機械の生産能力を調べるために、サンプリング手順を用いて生産された製品の品質を検査します。収集されたデータは次の通りです。

　　この業界の一般的なルールによると、標本の14個のデータ項目の分散が0.005を超える場合、その機械は修理のために停止させなければなりません。このときの機械は停止させなければならないでしょうか。

　　解：与えられたデータから、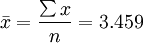を計算します。

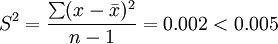
　　したがって、この機械は正常に動作しています。

　　分散と標準偏差もすべてのデータから計算され、各データがその平均値と比べて平均的にどれだけ離れているかを反映しているので、データのばらつきの程度を正確に反映することができます。分散と標準偏差は、実際に最も広く使われているばらつきの測度値です。